Équations

L'ellipse de base est l'ellipse centrée à l'origine, dont les sommets sont [latex]S_1(a, 0)[/latex] et [latex]S_2(−a, 0)[/latex] sur l'axe des abscisses et [latex]S_3(0, b)[/latex] et [latex]S_4(0, −b)[/latex] sur l'axe des ordonnées; les foyers sont les points de coordonnées [latex]F_1(c, 0)[/latex] et [latex]F_2(−c, 0)[/latex]. Si l'ellipse est centrée à l'origine, on obtient alors les données suivantes :

• [latex]\dfrac{x^2}{a^2}[/latex] + [latex]\dfrac{y^2}{b^2}[/latex] = 1 où [latex]{c^2}[/latex] = [latex]{a^2}[/latex] – [latex]{b^2}[/latex] si l'axe transversal est l'axe des abscisses :

les coordonnées du centre de l'ellipse sont : C(0, 0) les coordonnées de ses foyers sont : F[latex]_{1}[/latex](c, 0) et F[latex]_{2}[/latex](−c, 0) les coordonnées de ses sommets sur l'axe transversal sont : S[latex]_{1}[/latex](a, 0) et S[latex]_{2}[/latex](−a, 0) les coordonnées de ses sommets sur l'axe conjugué sont : S[latex]_{3}[/latex](0, b) et S[latex]_{4}[/latex](0,−b)

 

• [latex]\dfrac{y^2}{a^2}[/latex] + [latex]\dfrac{x^2}{b^2}[/latex] = 1 où [latex]{c^2}[/latex] = [latex]{a^2}[/latex] – [latex]{b^2}[/latex], si l'axe transversal est l'axe des ordonnées :

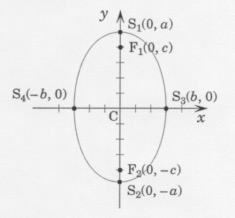
les coordonnées du centre de l'ellipse sont : C(0, 0) les coordonnées de ses foyers sont : F[latex]_{1}[/latex](0, c) et F[latex]_{2}[/latex](0, −c) les coordonnées de ses sommets sur l'axe transversal sont : S[latex]_{1}[/latex](0, a) et S[latex]_{2}[/latex](0, −a) les coordonnées de ses sommets sur l'axe conjugué sont : S[latex]_{3}[/latex](b, 0) et S[latex]_{4}[/latex](−b, 0)

Si l'ellipse n’est pas centrée à l'origine, on obtient alors les données suivantes :

• [latex]\dfrac{(x\space –\space h)^2}{a^2}[/latex] + [latex]\dfrac{(y\space –\space k)^2}{b^2}[/latex] = 1, pour une ellipse dont l'axe transversal est parallèle à l'axe des abscisses :

les coordonnées du centre de l'ellipse sont : C(h, k) les coordonnées de ses foyers sont : F[latex]_{1}[/latex](c + h, k) et F[latex]_{2}[/latex](−c + h, k) les coordonnées de ses sommets sur l'axe transversal sont : S[latex]_{1}[/latex](a + h, k) et S[latex]_{2}[/latex](−a + h, k) les coordonnées de ses sommets sur l'axe conjugué sont : S[latex]_{3}[/latex](h, b + k) et S[latex]_{4}[/latex](h,−b + k)

• [latex]\dfrac{(y\space –\space k)^2}{a^2}[/latex] + [latex]\dfrac{(x\space –\space h)^2}{b^2}[/latex] = 1, pour une ellipse dont l'axe transversal est parallèle à l'axe des ordonnées :

les coordonnées du centre de l'ellipse sont : C(h, k) les coordonnées de ses foyers sont : F[latex]_{1}[/latex](h, c + k) et F[latex]_{2}[/latex](h,−c + k) les coordonnées de ses sommets sur l'axe transversal sont : S[latex]_{1}[/latex](h, a + k) et S[latex]_{2}[/latex](h,−a + k) les coordonnées de ses sommets sur l'axe conjugué sont : S[latex]_{3}[/latex](b + h, k) et S[latex]_{4}[/latex](−b + h, k)