Equations

The standard ellipse is the ellipse centered at the origin, whose vertices are [latex]S_1(a, 0)[/latex] and [latex]S_2(−a, 0)[/latex] on the x-axis and [latex]S_3(0, b)[/latex] and [latex]S_4(0, −b)[/latex] on the y-axis; its foci are the points with coordinates [latex]F_1(c, 0)[/latex] and [latex]F_2(−c, 0)[/latex]. If the ellipse is centred at the origin, the equations are the following:

• [latex]\dfrac{x^2}{a^2}[/latex] + [latex]\dfrac{y^2}{b^2}[/latex] = 1, where [latex]{c^2}[/latex] = [latex]{a^2}[/latex] – [latex]{b^2}[/latex] if the transverse axis is the x-axis:

The coordinates of the centre of the ellipse are: C(0, 0) The coordinates of its foci are: F[latex]_{1}[/latex](c, 0) and F[latex]_{2}[/latex](−c, 0) The coordinates of its vertices on the transverse axis are: S[latex]_{1}[/latex](a, 0) and S[latex]_{2}[/latex](−a, 0) The coordinates of its vertices on the conjugate axis are: S[latex]_{3}[/latex](0, b) and S[latex]_{4}[/latex](0,−b)

 

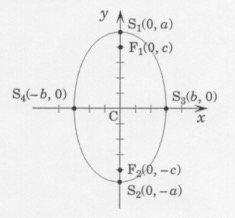
• [latex]\dfrac{y^2}{a^2}[/latex] + [latex]\dfrac{x^2}{b^2}[/latex] = 1, where [latex]{c^2}[/latex] = [latex]{a^2}[/latex] – [latex]{b^2}[/latex], if the transverse axis is the y-axis:

The coordinates of the centre of the ellipse are: C(0, 0) The coordinates of its foci are: F[latex]_{1}[/latex](0, c) and F[latex]_{2}[/latex](0, −c) The coordinates of its vertices on the transverse axis are: S[latex]_{1}[/latex](0, a) and S[latex]_{2}[/latex](0, −a) The coordinates of its vertices on the conjugate axis are: S[latex]_{3}[/latex](b, 0) and S[latex]_{4}[/latex](−b, 0)

If the ellipse is not centred at the origin, the following data is obtained:

• [latex]\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1[/latex], for an ellipse whose transverse axis is parallel to the x-axis:

The coordinates of the centre of the ellipse are: C(h,k). The coordinates of its foci are: F[latex]_{1}[/latex](c + h, k) and F[latex]_{2}[/latex](−c + h, k). The coordinates of its vertices on the transverse axis are: S[latex]_{1}[/latex](a + h, k) and S[latex]_{2}[/latex](−a + h, k). The coordinates of its vertices on the conjugate axis are: S[latex]_{3}[/latex](h, b + k) and S[latex]_{4}[/latex](h,−b + k).

• [latex]\frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1[/latex], for an ellipse whose transverse axis is parallel to the y-axis:

The coordinates of its foci are: C(h, k) The coordinates of its foci are: F[latex]_{1}[/latex](h, c + k) and F[latex]_{2}[/latex](h,−c + k) The coordinates of its vertices on the transverse axis are: S[latex]_{1}[/latex](h, a + k) and S[latex]_{2}[/latex](h,−a + k) The coordinates of its vertices on the conjugate axis are: S[latex]_{3}[/latex](b + h, k) and S[latex]_{4}[/latex](−b + h, k)